Contoh permutasi: Ada sebuah kotak berisi 3 bola masing-masing berwarna merah, hijau dan biru. Jika seorang anak ditugaskan untuk mengambil 2 bola secara acak dan urutan pengambilan diperhatikan, ada berapa permutasi yang terjadi?
Solusi: Ada 6 permutasi yaitu; M-H, M-B, H-M, H-B, B-M, B-H.
cat: terdapat n! permutasi dari n unsur yang berbeda, contoh: tentukan permutasi dari 3 unsur yang berbeda ABC? ada 6 permutasi.
Kombinasi adalah menggabungkan beberapa objek dari suatu grup tanpa memperhatikan urutan. Di dalam kombinasi, urutan tidak diperhatikan. {1,2,3} adalah sama dengan {2,3,1} dan {3,1,2}.
Contoh kombinasi: Seorang anak hanya diperbolehkan mengambil dua buah amplop dari tiga buah amplop yang disediakan yaitu amplop A, amplop B dan amplop C. Tentukan ada berapa banyak kombinasi untuk mengambil dua buah amplop dari tiga buah amplop yang disediakan?
Solusi: Ada 3 kombinasi yaitu; A-B, A-C dan B-C.
Permutasi Pengulangan
Jika urutan diperhatikan dan suatu objek dapat dipilih lebih dari sekali maka jumlah permutasinya adalah:
Sebagai contoh, jika kamu memiliki huruf A, B, C, dan D dan kamu ingin mencari tahu ada berapa cara untuk menyusunnya dalam suatu grup yang berisi tiga angka maka kamu akan menemukan bahwa ada 43 atau 64 cara untuk menyusunnya. Beberapa cara untuk menyusunnya adalah: AAA, BBB, CCC, DDD, ABB, CBB, DBB, dst.
Permutasi Tanpa Pengulangan
Jika urutan diperhatikan dan setiap objek yang tersedia hanya bisa dipilih atau dipakai sekali maka jumlah permutasi yang ada adalah:Terkadang kita hanya ingin menyusun ulang sejumlah elemen saja, tidak semuanya. Permutasi ini disebut permutasi-k dari n benda
contoh:
1. Pada untai abcd, maka permutasi-2 dari abcd (yang semuanya ada 4 unsur) adalah sebanyak 12 (4!/(4-2)!) : ab ac ad ba bc bd ca cb cd da db dc. Sedangkan permutasi-3 dari untai yang sama adalah sebanyak 24: abc abd acb acd adb adc bac bca bad bda bcd bdc cab cba cad cda cbd cdb dab dba dac dca dbc dcb.
2. Ada sebuah pemungutan suara dalam suatu organisasi. Kandidat yang bisa dipilih ada lima orang. Yang mendapat suara terbanyak akan diangkat menjadi ketua organisasi tersebut. Yang mendapat suara kedua terbanyak akan diangkat menjadi wakil ketua. Dan yang mendapat suara ketiga terbanyak akan menjadi sekretaris. Ada berapa banyak hasil pemungutan suara yang mungkin terjadi? Dengan menggunakan rumus di atas maka ada 5!/(5-3)! = 60 permutasi.
3. Berapa banyaknya permutasi dari cara duduk yang dapat terjadi jika 8 orang disediakan 4 kursi, sedangkan salah seorang dari padanya selalu duduk dikursi tertentu?
Jika salah seorang selalu duduk dikursi tertentu maka tinggal 7 orang dengan 3 kursi kosong.Maka banyaknya cara duduk ada :
7P3 = 7!/(7-3)! = 7!/4! = 7.6.5 = 210 cara
4. Ada lima kotak kosong yang tersedia. Kelima kotak kosong itu harus diisi (tidak boleh ada yang kosong). Kelima kotak kosong itu hanya boleh diisi dengan angka 1,2,3,4,5. Ada berapa banyak cara untuk mengisi kotak kosong? Dengan menggunakan rumus n! maka ada 5! = 120 permutasi.
cat: 0! = 1! = 1
Permutasi dengan Elemen yang Identik
Terkadang tidak semua unsur dalam permutasi dapat dibedakan. Unsur-unsur ini adalah unsur-unsur yang identik atau sama secara kualitas. Suatu untai aabc terdiri dari 4 macam unsur, yaitu a, b, dan c tetapi unsur a muncul sebanyak dua kali. Kedua a tersebut identik. Permutasi dari aabc adalah berjumlah 12:
aabc aacb abac abca acab acba baac baca bcaa caab caba cbaaIni bisa dimengerti sebagai permutasi biasa dengan kedua unsur a dibedakan, yaitu a0 dan a1:
a0a1bc a1a0bc = aabc a0a1cb a1a0cb = aacb a0ba1c a1ba0c = abac a0bca1 a1bca0 = abca a0ca1b a1ca0b = acab a0cba1 a1cba0 = acba ba0a1c ba1a0c = baac ba0ca1 ba1ca0 = baca bca0a1 bca1a0 = bcaa ca0a1b ca1a0b = caab ca0ba1 ca1ba0 = caba cba0a1 cba1a0 = cbaaTotal permutasi dari untai aabc adalah sebanyak 4! = 24. Tetapi total permutasi ini juga mencakup posisi a0 dan a1 yang bertukar-tukar, yang jumlahnya adalah 2! (karena a terdiri dari 2 unsur: a0 dan a1). Dengan demikian jika dianggap a0 = a1 maka banyak permutasinya menjadi 4! dibagi dengan 2!. Cara menghitung ini dapat digeneralisasikan:
Untuk untai S sepanjang n yang mengandung satu macam unsur identik sebanyak k:
Lebih general lagi, jika panjang untai adalah n, mengandung m macam unsur yang masing-masing adalah sebanyak k1, k2, ..., km, maka:
atau
Contoh:
untai aaaaabbcccdddddd terdiri dari 5 a, 2 b, 3 c, dan 6 d, maka banyaknya permutasi yang dapat dibentuk:
Dalam permutasi biasa, misalnya abcd, setiap unsur hanya muncul satu kali, sehingga
Unsur yang identik tersebut tidak perlu benar-benar identik, tetapi bisa merupakan unsur yang berbeda, tetapi ada kualitas tertentu yang kita anggap sama dari kedua unsur tersebut. Sebagai contoh, huruf A dan huruf a bisa dianggap identik untuk keperluan tertentu.
Permutasi siklis
Permutasi siklis menganggap elemen disusun secara melingkar.
h a g b f c e dPada susunan di atas, kita dapat membaca untai tersebut sebagai salah satu dari untai-untai berikut:
abcdefgh bcdefgha cdefghab defghabc efghabcd fghabcde ghabcdef habcdefgCara membaca untai abcdefgh dalam susunan melingkar tersebut bermacam-macam, maka setiap macam cara kita anggap identik satu sama lain. Permutasi siklis dapat dihitung dengan menganggap bahwa satu elemen harus ditulis sebagai awal untai.
Dengan menganggap panjang untai (atau banyaknya elemen) adalah n, dan karena elemen awal tidak boleh diubah-ubah posisinya, maka banyaknya elemen yang dapat berubah-ubah posisinya adalah n-1. Dengan demikian kita cukup mempermutasikan elemen yang dapat berubah-ubah posisi saja, yaitu sebanyak  .
.
contoh:
Ada berapa cara 7 orang yang duduk mengelilingi meja dapat menempati ketujuh tempat duduk dengan urutan yang berlainan?
Banyaknya cara duduk ada (7 - 1) ! = 6 ! = 6 . 5 . 4. 3 . 2 . 1 = 720 cara.
Kombinasi Tanpa Pengulangan
Ketika urutan tidak diperhatikan akan tetapi setiap objek yang ada hanya bisa dipilih sekali maka jumlah kombinasi yang ada adalah:contoh:
kamu mempunyai 5 pensil warna dengan warna yang berbeda yaitu; merah, kuning, hijau, biru dan ungu. Kamu ingin membawanya ke sekolah. Tapi kamu hanya boleh membawa dua pensil warna. Ada berapa banyak cara untuk mengkombinasikan pensil warna yang ada? Dengan menggunakan rumus di atas maka ada 5!/(5-2)!(2)! = 10 kombinasi.
Kombinasi pengulangan
Jika urutan tidak diperhatikan dan objek bisa dipilih lebih dari sekali, maka jumlah kombinasi yang ada adalah:contoh:
jika kamu pergi ke sebuah toko donat. Toko donut itu menyediakan 10 jenis donat berbeda. Kamu ingin membeli tiga donat. Maka kombinasi yang dihasilkan adalah (10+3-1)!/3!(10-1)! = 220 kombinasi.

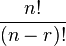


Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.