Dalam matematika, bilangan kompleks adalah bilangan yang berbentuk
dimana a dan b adalah bilangan riil, dan i adalah bilangan imajiner tertentu yang mempunyai sifat i 2 = −1. Bilangan riil a disebut juga bagian riil dari bilangan kompleks, dan bilangan real b disebut bagian imajiner. Jika pada suatu bilangan kompleks, nilai b adalah 0, maka bilangan kompleks tersebut menjadi sama dengan bilangan real a.
Sebagai contoh, 3 + 2i adalah bilangan kompleks dengan bagian riil 3 dan bagian imajiner 2.
Bilangan kompleks dapat ditambah, dikurang, dikali, dan dibagi seperti bilangan riil; namun bilangan kompleks juga mempunyai sifat-sifat tambahan yang menarik. Misalnya, setiap persamaan aljabar polinomial mempunyai solusi bilangan kompleks, tidak seperti bilangan riil yang hanya memiliki sebagian.
Dalam bidang-bidang tertentu (seperti teknik elektro, dimana i digunakan sebagai simbol untuk arus listrik), bilangan kompleks ditulis a + bj.
1. Definisi
2. Notasi
3. Bidang kompleks
4. Lihat pula
1. Definisi
1. 1. Notasi dan operasi
Himpunan bilangan kompleks umumnya dinotasikan dengan C, atau  . Bilangan real, R, dapat dinyatakan sebagai bagian dari himpunan C dengan menyatakan setiap bilangan real sebagai bilangan kompleks:
. Bilangan real, R, dapat dinyatakan sebagai bagian dari himpunan C dengan menyatakan setiap bilangan real sebagai bilangan kompleks:  .
.
Bilangan kompleks ditambah, dikurang, dan dikali dengan menggunakan sifat-sifat aljabar seperti asosiatif, komutatif, dan distributif, dan dengan persamaan i 2 = −1:
- (a + bi) + (c + di) = (a+c) + (b+d)i
- (a + bi) − (c + di) = (a−c) + (b−d)i
- (a + bi)(c + di) = ac + bci + adi + bd i 2 = (ac−bd) + (bc+ad)i
Pembagian bilangan kompleks juga dapat didefinisikan (lihat dibawah). Jadi, himpunan bilangan kompleks membentuk bidang matematika yang, berbeda dengan bilangan real, berupa aljabar tertutup.
Dalam matematika, adjektif "kompleks" berarti bilangan kompleks digunakan sebagai dasar teori angka yang digunakan. Sebagai contoh, analisis kompleks, matriks kompleks, polinomial kompleks, dan aljabar Lie kompleks.
1. 2. Definisi
Definisi formal bilangan kompleks adalah sepasang bilangan real (a, b) dengan operasi sebagai berikut:
Dengan definisi diatas, bilangan-bilangan kompleks yang ada membentuk suatu himpunan bilangan kompleks yang dinotasikan dengan C.
Karena bilangan kompleks a + bi merupakan spesifikasi unik yang berdasarkan sepasang bilangan riil (a, b), bilangan kompleks mempunyai hubungan korespondensi satu-satu dengan titik-titik pada satu bidang yang dinamakan bidang kompleks.
Bilangan riil a dapat disebut juga dengan bilangan kompleks (a, 0), dan dengan cara ini, himpunan bilangan riil R menjadi bagian dari himpunan bilangan kompleks C.
Dalam C, berlaku sebagai berikut:
- identitas penjumlahan ("nol"): (0, 0)
- identitas perkalian ("satu"): (1, 0)
- invers penjumlahan (a,b): (−a, −b)
- invers perkalian (reciprocal) bukan nol (a, b):
2. Notasi
2. 1. Bentuk Penjumlahan
Bilangan kompleks pada umumnya dinyatakan sebagai penjumlahan dua suku, dengan suku pertama adalah bilangan riil, dan suku kedua adalah bilangan imajiner.
2. 2. Bentuk Polar
Dengan menganggap bahwa:
dan
maka
Untuk mempersingkat penulisan, bentuk  juga sering ditulis sebagai
juga sering ditulis sebagai  .
.
2. 3. Bentuk Eksponen
Bentuk lain adalah bentuk eksponen, yaitu:
3. Bidang kompleks

Bilangan kompleks dapat divisualisasikan sebagai titik atau vektor posisi pada sistem koordinat dua dimensi yang dinamakan bidang kompleks atau Diagram Argand.
Koordinat Cartesian bilangan kompleks adalah bagian riil x dan bagian imajiner y, sedangkan koordinat sirkularnya adalah r = |z|, yang disebut modulus, dan φ = arg(z), yang disebut juga argumen kompleks dari z (Format ini disebut format mod-arg). Dikombinasikan dengan Rumus Euler, dapat diperoleh:
Kadang-kadang, notasi r cis φ dapat juga ditemui.
Perlu diperhatikan bahwa argumen kompleks adalah unik modulo 2π, jadi, jika terdapat dua nilai argumen kompleks yang berbeda sebanyak kelipatan bilangan bulat dari 2π, kedua argumen kompleks tersebut adalah sama (ekivalen).
Dengan menggunakan identitas trigonometri dasar, dapat diperoleh:
dan
Penjumlahan dua bilangan kompleks sama seperti penjumlahan vektor dari dua vektor, dan perkalian dengan bilangan kompleks dapat divisualisasikan sebagai rotasi dan pemanjangan secara bersamaan.
Perkalian dengan i adalah rotasi 90 derajat berlawanan dengan arah jarum jam ( radian). Secara geometris, persamaan i2 = −1 adalah dua kali rotasi 90 derajat yang sama dengan rotasi 180 derajat (
radian). Secara geometris, persamaan i2 = −1 adalah dua kali rotasi 90 derajat yang sama dengan rotasi 180 derajat ( radian).
radian).
Lingkaran yang paling besar itu menunjukkan himpunan bilangan kompleks, memperlihatkan betapa luasnya himpunan bilangan kompleks. Hmm.. Di post ini, kita akan mengenal bilangan kompleks. Tapi, hanya dasarnya saja. Untuk pengembangan lebih lanjut, akan kupost kapan2.. hahaha.. XD
=========================================================================
BAGIAN I
DEFINISI BILANGAN KOMPLEKS
DEFINISI BILANGAN KOMPLEKS
Dari prakata di atas, kita tahu bahwa bilangan kompleks adalah gabungan antara bilangan Real dengan bilangan Imajiner.
Sekilas tentang bilangan imajiner.
Bilangan imajiner adalah bilangan yang merupakan akar kuadrat dari suatu bilangan negatif. Misalnya, ,
,  ,
,  , dan masih banyak lagi..
, dan masih banyak lagi..
Lalu, di sini kita akan berurusan dengan bilangan . Kita definisikan bahwa
. Kita definisikan bahwa  =
=  , maka:
, maka:
Oleh karena itu, dapat kita tulis juga menjadi
dapat kita tulis juga menjadi 
 , maka dapat ditulis sebagai
, maka dapat ditulis sebagai 
 .
.
Banyak sekali orang yang keliru mengoperasikan bilangan imajiner.
Misalnya:

 =
=  =
=  = 5. (ini salah!!)
= 5. (ini salah!!)
Seharusnya:

 =
= 



 = 5.
= 5. = (
= ( 1).5 =
1).5 =  5
5
Untuk menghindari kesalahan, selalu konversikan bilangan imajiner ke dalam bentuk (ini dinamakan sebagai bentuk standar). ^^
(ini dinamakan sebagai bentuk standar). ^^
Simbol mempunyai sifat
mempunyai sifat  =
=  =
=  1. Untuk pangkat yang lebih tinggi, kita tinggal ngotak-ngatik.
1. Untuk pangkat yang lebih tinggi, kita tinggal ngotak-ngatik.  =
= 

 =
= 
 . Lalu,
. Lalu,  =
= 

 = 1. Untuk seterusnya, silakan dicoba sendiri. ^^. Not difficult.
= 1. Untuk seterusnya, silakan dicoba sendiri. ^^. Not difficult.
Bilangan imajiner adalah bilangan yang merupakan akar kuadrat dari suatu bilangan negatif. Misalnya,
 ,
,  ,
,  , dan masih banyak lagi..
, dan masih banyak lagi..Lalu, di sini kita akan berurusan dengan bilangan
 . Kita definisikan bahwa
. Kita definisikan bahwa  =
=  , maka:
, maka:Oleh karena itu,
 dapat kita tulis juga menjadi
dapat kita tulis juga menjadi 
 , maka dapat ditulis sebagai
, maka dapat ditulis sebagai 
 .
.Banyak sekali orang yang keliru mengoperasikan bilangan imajiner.
Misalnya:


 =
=  =
=  = 5. (ini salah!!)
= 5. (ini salah!!)Seharusnya:


 =
= 



 = 5.
= 5. = (
= ( 1).5 =
1).5 =  5
5Untuk menghindari kesalahan, selalu konversikan bilangan imajiner ke dalam bentuk
 (ini dinamakan sebagai bentuk standar). ^^
(ini dinamakan sebagai bentuk standar). ^^Simbol
 mempunyai sifat
mempunyai sifat  =
=  =
=  1. Untuk pangkat yang lebih tinggi, kita tinggal ngotak-ngatik.
1. Untuk pangkat yang lebih tinggi, kita tinggal ngotak-ngatik.  =
= 

 =
= 
 . Lalu,
. Lalu,  =
= 

 = 1. Untuk seterusnya, silakan dicoba sendiri. ^^. Not difficult.
= 1. Untuk seterusnya, silakan dicoba sendiri. ^^. Not difficult.NOTASI
Bilangan kompleks (z) terdiri dari gabungan bilangan Real dan Imajiner. Oleh karena itu, dapat kita notasikan dengan hubungan penjumlahan.
z = x + y
Notasi di atas menunjukkan bahwa x adalah bagian REAL, sedangkan y
 adalah bagian imajiner murni. Bilangan x dan y, keduanya adalah bilangan REAL.
adalah bagian imajiner murni. Bilangan x dan y, keduanya adalah bilangan REAL.Himpunan bilangan kompleks digambarkan pada bidang kompleks, dan suatu bilangan kompleks digambarkan dengan sebuah titik pada bidang kompleks. (Lebih mudahnya, ini seperti menggambar titik pada koordinat x dan y, di mana x merupakan bagian REAL, sedangkan y adalah bagian IMAJINER.)
Langsung saja kita ke contoh pemahaman.. Daripada nanti kebingungan.. ^^
Contoh Soal 1:
Ada 4 bilangan kompleks yang disimbolkan z1, z2, z3, dan z4.
z1 = 3 + 6 .
.
z2 = -3+2 .
.
z3 = -2-2 .
.
z4 = 4 - 3 .
.
Gambarkan titik-titik z1, z2, z3, dan z4 di bidang kompleks!
Jawab:
Kita buat koordinat x dan y, di mana z=x + y . 4 titik itu digambar sebagai berikut.
. 4 titik itu digambar sebagai berikut.
Contoh Soal 2:
Suatu bilangan kompleks z dinotasikan sebagai z = (x + y ).
).
Jika z = , tentukan x dan y. Lalu, gambarkan z dalam bidang kompleks!
, tentukan x dan y. Lalu, gambarkan z dalam bidang kompleks!
Jawab:
Bentuk z diubah dulu atau disederhanakan.. ^^
z =
z =
z =
z =
z =
Nah, di sini didapat bahwa x=5 dan y = .
.
Ini adalah lokasi titik z di bidang kompleks:
Contoh Soal 3 (pemahaman):
Bisakah kamu memberi contoh bilangan yang bukan bilangan kompleks?
Jawab:
Bilangan yang bukan kompleks adalah bilangan yang mengandung bilangan yang tidak imajiner dan tidak real juga.. Misalnya ,
,  , dan masih banyak lagi.. Tapi, ini yang masih menjadi kendala.. Apakah
, dan masih banyak lagi.. Tapi, ini yang masih menjadi kendala.. Apakah  ,
,  , dan sebagainya itu masih bisa disebut bilangan?? Sejauh saya belajar, tak pernah ada pembahasan mengenai bilangan nonkompleks...
, dan sebagainya itu masih bisa disebut bilangan?? Sejauh saya belajar, tak pernah ada pembahasan mengenai bilangan nonkompleks...
Contoh Soal 4 (pemahaman):
Suatu bilangan kompleks z dinotasikan sebagai z = (x + y ).
).
Tentukan nilai x dan y dari bilangan:
(i) 0
(ii)5
(iii)
Jawab:
(i) 0 = 0+ o . Jadi, x=0 dan y=0.
. Jadi, x=0 dan y=0.
(ii) 5 = 5+0 . Jadi, x=5 dan y=0.
. Jadi, x=5 dan y=0.
(iii) = 0+
= 0+ 
 . Jadi, x=0 dan y=
. Jadi, x=0 dan y= .
.
Contoh Soal 5:
Jika z1 = z2 = z3.
z1 = c + a .
.
z2 = b + 2c .
.
z3 = a+2 - d .
.
Tentukan a, b, c, d dan z1, z2, dan z3!
Jawab:
Di sini, kita harus tahu bahwa 2 bilangan kompleks p + q dan r+s
dan r+s dikatakan sama jika dan hanya jika p = r DAN q = s.
dikatakan sama jika dan hanya jika p = r DAN q = s.
Oleh karena itu, kita tinggal menghubung-hubungkan koefisiennya.. ^^
a = 2c = -d ... (ii)
c= a+2
Substitusikan nilai c ke persamaan 2
a = 2(a+2)
a = 2a + 4
a = -4
Secara otomatis, kita dapatkan nilai d = 4. c=-2. b = -2. (Substitusi biasa)
Kita dapatkan z1 = z2 = z3 = c + a = -2 -4
= -2 -4 .
.
Ada 4 bilangan kompleks yang disimbolkan z1, z2, z3, dan z4.
z1 = 3 + 6
 .
.z2 = -3+2
 .
.z3 = -2-2
 .
.z4 = 4 - 3
 .
.Gambarkan titik-titik z1, z2, z3, dan z4 di bidang kompleks!
Jawab:
Kita buat koordinat x dan y, di mana z=x + y
 . 4 titik itu digambar sebagai berikut.
. 4 titik itu digambar sebagai berikut.Contoh Soal 2:
Suatu bilangan kompleks z dinotasikan sebagai z = (x + y
 ).
).Jika z =
 , tentukan x dan y. Lalu, gambarkan z dalam bidang kompleks!
, tentukan x dan y. Lalu, gambarkan z dalam bidang kompleks!Jawab:
Bentuk z diubah dulu atau disederhanakan.. ^^
z =

z =

z =

z =

z =

Nah, di sini didapat bahwa x=5 dan y =
 .
.Ini adalah lokasi titik z di bidang kompleks:
Contoh Soal 3 (pemahaman):
Bisakah kamu memberi contoh bilangan yang bukan bilangan kompleks?
Jawab:
Bilangan yang bukan kompleks adalah bilangan yang mengandung bilangan yang tidak imajiner dan tidak real juga.. Misalnya
 ,
,  , dan masih banyak lagi.. Tapi, ini yang masih menjadi kendala.. Apakah
, dan masih banyak lagi.. Tapi, ini yang masih menjadi kendala.. Apakah  ,
,  , dan sebagainya itu masih bisa disebut bilangan?? Sejauh saya belajar, tak pernah ada pembahasan mengenai bilangan nonkompleks...
, dan sebagainya itu masih bisa disebut bilangan?? Sejauh saya belajar, tak pernah ada pembahasan mengenai bilangan nonkompleks...Contoh Soal 4 (pemahaman):
Suatu bilangan kompleks z dinotasikan sebagai z = (x + y
 ).
).Tentukan nilai x dan y dari bilangan:
(i) 0
(ii)5
(iii)

Jawab:
(i) 0 = 0+ o
 . Jadi, x=0 dan y=0.
. Jadi, x=0 dan y=0.(ii) 5 = 5+0
 . Jadi, x=5 dan y=0.
. Jadi, x=5 dan y=0.(iii)
 = 0+
= 0+ 
 . Jadi, x=0 dan y=
. Jadi, x=0 dan y= .
.Contoh Soal 5:
Jika z1 = z2 = z3.
z1 = c + a
 .
.z2 = b + 2c
 .
.z3 = a+2 - d
 .
.Tentukan a, b, c, d dan z1, z2, dan z3!
Jawab:
Di sini, kita harus tahu bahwa 2 bilangan kompleks p + q
 dan r+s
dan r+s dikatakan sama jika dan hanya jika p = r DAN q = s.
dikatakan sama jika dan hanya jika p = r DAN q = s.Oleh karena itu, kita tinggal menghubung-hubungkan koefisiennya.. ^^
z1 = z2 = z3
c + a = b + 2c
= b + 2c = a+2 - d
= a+2 - d .
.
c = b = a+2 ... (i) = b + 2c
= b + 2c = a+2 - d
= a+2 - d .
.a = 2c = -d ... (ii)
c= a+2
Substitusikan nilai c ke persamaan 2
a = 2(a+2)
a = 2a + 4
a = -4
Secara otomatis, kita dapatkan nilai d = 4. c=-2. b = -2. (Substitusi biasa)
Kita dapatkan z1 = z2 = z3 = c + a
 = -2 -4
= -2 -4 .
.=========================================================================
BAGIAN II
OPERASI BILANGAN KOMPLEKS
Di sini akan dijelaskan operasi bilangan kompleks yang meliputi penjumlahan, pengurangan, perkalian, dan pembagian.. Langsung ke contoh soal.
Contoh Soal 6 (penjumlahan):
(3+2 )+(-2+7
)+(-2+7 ) =....
) =....
Jawab:
(3+2 )+(-2+7
)+(-2+7 ) = 3 + 2
) = 3 + 2 -2 + 7
-2 + 7 = 1 + 9
= 1 + 9 .
.
Contoh Soal 7 (pengurangan):
(2-3 )-(8-2
)-(8-2 )=....
)=....
Jawab:
Dikerjakan sama seperti penjumlahan..
(2-3 )-(8-2
)-(8-2 ) = 2 -3
) = 2 -3 -8 +2
-8 +2 = -6 -
= -6 - .
.
Contoh Soal 8 (perkalian):
(3+4 )(2-5
)(2-5 ) = ....
) = ....
Jawab:
Lakukan perkalian biasa terlebih dahulu.
(3+4 )(2-5
)(2-5 ) = 6 -15
) = 6 -15 + 8
+ 8 -20
-20 .
.
Lalu ubah menjadi
menjadi  1.(3+4
1.(3+4 )(2-5
)(2-5 ) = 6 -15
) = 6 -15 + 8
+ 8 +20 = 26 -7
+20 = 26 -7 .
.
Contoh Soal 9 (pembagian):
 = ....
= ....
Jawab:
Lihat bagian penyebut, yaitu 3+4i. Maka, sekawan/konjugatnya adalah 3-4i. Kalikan bilangan konjugat ini di pembilang dan penyebut.. (lihat langkah di bawah).
 =
= 


====-=
====-=
====-=
====-=
Contoh Soal 10 (pemangkatan Sederhana):
Jika z = 3- . Tentukan
. Tentukan  .
.
Jawab:
Hasil dari pemangkatan dapat diselesaikan dengan dalil De Moivre. Namun, karena kita belum belajar hal itu, kita akan mengalikannya secara biasa.
 = (3-
= (3- )(3-
)(3- )(3-
)(3- ) = (9-6
) = (9-6 -1)(3-
-1)(3- )=(8-6
)=(8-6 )(3-
)(3- )=24-8
)=24-8 -18
-18 -6=18-27
-6=18-27 .
.
(3+2
 )+(-2+7
)+(-2+7 ) =....
) =....Jawab:
(3+2
 )+(-2+7
)+(-2+7 ) = 3 + 2
) = 3 + 2 -2 + 7
-2 + 7 = 1 + 9
= 1 + 9 .
.Contoh Soal 7 (pengurangan):
(2-3
 )-(8-2
)-(8-2 )=....
)=....Jawab:
Dikerjakan sama seperti penjumlahan..
(2-3
 )-(8-2
)-(8-2 ) = 2 -3
) = 2 -3 -8 +2
-8 +2 = -6 -
= -6 - .
.Contoh Soal 8 (perkalian):
(3+4
 )(2-5
)(2-5 ) = ....
) = ....Jawab:
Lakukan perkalian biasa terlebih dahulu.
(3+4
 )(2-5
)(2-5 ) = 6 -15
) = 6 -15 + 8
+ 8 -20
-20 .
.Lalu ubah
 menjadi
menjadi  1.(3+4
1.(3+4 )(2-5
)(2-5 ) = 6 -15
) = 6 -15 + 8
+ 8 +20 = 26 -7
+20 = 26 -7 .
.Contoh Soal 9 (pembagian):
 = ....
= ....Jawab:
Lihat bagian penyebut, yaitu 3+4i. Maka, sekawan/konjugatnya adalah 3-4i. Kalikan bilangan konjugat ini di pembilang dan penyebut.. (lihat langkah di bawah).
 =
= 


====-=

====-=

====-=

====-=

Contoh Soal 10 (pemangkatan Sederhana):
Jika z = 3-
 . Tentukan
. Tentukan  .
.Jawab:
Hasil dari pemangkatan dapat diselesaikan dengan dalil De Moivre. Namun, karena kita belum belajar hal itu, kita akan mengalikannya secara biasa.
 = (3-
= (3- )(3-
)(3- )(3-
)(3- ) = (9-6
) = (9-6 -1)(3-
-1)(3- )=(8-6
)=(8-6 )(3-
)(3- )=24-8
)=24-8 -18
-18 -6=18-27
-6=18-27 .
.=========================================================================
Note: bilangan kompleks jika digunakan di koordinat polar dapat menjadi sangat fleksibel dan *luar biasa*.. Di sini, akan muncul "Dalil Moivre" juga. Rumus-rumus euler dapat diturunkan dari definisi bilangan kompleks di koordinat polar.
Bilangan Kompleks... (ii) {Dalil De Moivre}
Post ini adalah lanjutan dari posting mengenai Mengenal Bilangan Kompleks.. Sebetulnya, aku agak ragu dengan post ini. Pertama, ini adalah materi kuliah.. Pasti banyak dari kalian yang menganggap bahwa ini post yang "menyebalkan". Ada yang bilang bahwa "Matematika itu Sucks". Ada yang bilang bahwa "Matematika itu tidak penting"... Hmm.. Melalui bilangan kompleks kita bisa melihat *keistimewaan matematika* di materi ini. Persamaan euler adalah salah satu contoh hasil dari pengembangan bilangan kompleks.. Yach, bagi yang tidak mau melihat post ini, silakan ditinggalkan. Tapi, bagi yang penasaran akan *keajaiban matematika*, silakan dilanjutkan. ^^
Di sini akan dijelaskan mengenai Dalil De Moivre.. Tapi, alangkah baiknya kalau kita mengenal dulu konsep bilangan kompleks dalam polar.. ^^
=========================================================================
z = x+y dapat digambarkan dalam bidang kompleks. Artinya, kita dapat menggambarkannya secara kartesius maupun polar!! Lihat gambar di bawah untuk lebih jelasnya!
dapat digambarkan dalam bidang kompleks. Artinya, kita dapat menggambarkannya secara kartesius maupun polar!! Lihat gambar di bawah untuk lebih jelasnya!
Jika titik z digambarkan secara kartesius tentunya kita akan mengatakan bahwa titik itu berada di koordinat (x,y). Namun, jika berbicara di koordinat polar, kita akan mengatakan bahwa titik z berada di (r, ), arah
), arah  dengan panjang r. Di sini,
dengan panjang r. Di sini,  adalah sudut yang dihitung dari sumbu x positif berputar berlawanan dengan arah jarum jam (tentunya ini materi SMA yang sebenarnya tidak perlu dijelaskan lagi).
adalah sudut yang dihitung dari sumbu x positif berputar berlawanan dengan arah jarum jam (tentunya ini materi SMA yang sebenarnya tidak perlu dijelaskan lagi).
 disebut sebagai argumen z, sedangkan r disebut sebagai modulus (panjang) z.
disebut sebagai argumen z, sedangkan r disebut sebagai modulus (panjang) z.
Kembali lihat gambar di atas.



=========================================================================
Misalkan kita punya bilangan kompleks z1 dan z2 dimana:


Sekarang, kita akan mencoba mengalikan keduanya...



Lihatlah bagian yang bisa digabung.... Lalu, persamaan itu *secara ajaib* menjadi:


Disingkat menjadi:


Dengan sendirinya,
 .
.
Jika , maka kita akan menemukan dalil de Moivre:
, maka kita akan menemukan dalil de Moivre:

n bilangan bulat..
Catatan: Perkalian-perpangkatan/pengambilan akar-pembagian bilangan-bilangan kompleks akan cepat dilakukan dengan menggunakan sistem polar, apabila argumen-argumen bilangan kompleks tersebut merupakan sudut-sudut kelipatan dari atau
atau  .
.
=========================================================================
Selesai sudah bagian Dalil De Moivre, bilangan kompleks bagian kedua...!! XD
Mudah bukan?? Post ini adalah revisi kedua, setelah sebelumnya ada kesesatan menggunakan dalil De Moivre di mana nilai n-nya boleh pecahan (di contoh soal nomor 3 dan 4).. Ingat, dalil de Moivre hanya berfungsi jika n adalah bilangan bulat.. So, post ini aku rombak ulang agar tidak menggunakan cara yang menyesatkan (meskipun jawaban di post sebelumnya tidak salah, namun ini hanya di dalam kasus khusus yang demikian, dan tidak akan dibahas di sini.) ^^
Di sini akan dijelaskan mengenai Dalil De Moivre.. Tapi, alangkah baiknya kalau kita mengenal dulu konsep bilangan kompleks dalam polar.. ^^
=========================================================================
BAGIAN III
BILANGAN KOMPLEKS DALAM POLAR
Perhatikan post sebelumnya!!z = x+y
 dapat digambarkan dalam bidang kompleks. Artinya, kita dapat menggambarkannya secara kartesius maupun polar!! Lihat gambar di bawah untuk lebih jelasnya!
dapat digambarkan dalam bidang kompleks. Artinya, kita dapat menggambarkannya secara kartesius maupun polar!! Lihat gambar di bawah untuk lebih jelasnya!Jika titik z digambarkan secara kartesius tentunya kita akan mengatakan bahwa titik itu berada di koordinat (x,y). Namun, jika berbicara di koordinat polar, kita akan mengatakan bahwa titik z berada di (r,
 ), arah
), arah  dengan panjang r. Di sini,
dengan panjang r. Di sini,  adalah sudut yang dihitung dari sumbu x positif berputar berlawanan dengan arah jarum jam (tentunya ini materi SMA yang sebenarnya tidak perlu dijelaskan lagi).
adalah sudut yang dihitung dari sumbu x positif berputar berlawanan dengan arah jarum jam (tentunya ini materi SMA yang sebenarnya tidak perlu dijelaskan lagi). disebut sebagai argumen z, sedangkan r disebut sebagai modulus (panjang) z.
disebut sebagai argumen z, sedangkan r disebut sebagai modulus (panjang) z.Notasi:
mod.(z)= r
arg.(z) =
mod.(z)= r
arg.(z) =

Kembali lihat gambar di atas.



Oleh karena itu,
z_= x+y
z_=
z_=
Disingkat menjadi
z =
Dapat dikatakan juga:

z_= x+y

z_=

z_=

Disingkat menjadi
z =

Dapat dikatakan juga:

Lihat kembali gambar di atas, bilangan kompleks z = x+y secara geometris dapat dinyatakan cengan vektor posisi.!!
secara geometris dapat dinyatakan cengan vektor posisi.!!
Operasi bilangan kompleks secara geometris dalam bentuk vektor dapat dilakukan sebagai berikut (z1 dan z2 diketahui):
 secara geometris dapat dinyatakan cengan vektor posisi.!!
secara geometris dapat dinyatakan cengan vektor posisi.!!Operasi bilangan kompleks secara geometris dalam bentuk vektor dapat dilakukan sebagai berikut (z1 dan z2 diketahui):
=========================================================================
BAGIAN IV
DALIL DE MOIVRE
Dengan sistem polar mempermudah perkalian dan pembagian bilangan-bilangan kompleks.Misalkan kita punya bilangan kompleks z1 dan z2 dimana:


Sekarang, kita akan mencoba mengalikan keduanya...



Lihatlah bagian yang bisa digabung.... Lalu, persamaan itu *secara ajaib* menjadi:


Disingkat menjadi:


Dengan sendirinya,

 .
.Jika
 , maka kita akan menemukan dalil de Moivre:
, maka kita akan menemukan dalil de Moivre:
n bilangan bulat..
Note: Bagaimana jika kita melakukan pembagian bilangan kompleks z1 dan z2? Maka, akan menghasilkan rumus:  .. Cobalah sendiri.. ^^
.. Cobalah sendiri.. ^^
 .. Cobalah sendiri.. ^^
.. Cobalah sendiri.. ^^Catatan: Perkalian-perpangkatan/pengambilan akar-pembagian bilangan-bilangan kompleks akan cepat dilakukan dengan menggunakan sistem polar, apabila argumen-argumen bilangan kompleks tersebut merupakan sudut-sudut kelipatan dari
 atau
atau  .
.Contoh Soal 1:
 .
.
Hitunglah .
.
Jawab:
Seandainya kita tidak mau menggunakan dalil de Moivre pun, kita bisa mengerjakan soal ini secara *tradisional*.. Yaitu dengan mengalikannya satu per satu.
 =
=  =
=  =
= 
Nah, bagaimana jika kita ingin mengerjakannnya secara dalil de Moivre? Akan lebih mengerti jika kita menggambar titik z itu.. (Ini supaya kita lebih mengerti saja.. Tapi, tidak mutlak)
 r =
r =  =
= 
 ---->
---->  (karena terletak di kuadran 4...)
(karena terletak di kuadran 4...)

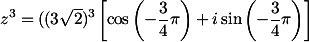
 =
=  .
.
Hasilnya sama, bukan?
Contoh Soal 2:

Hitunglah .
.
Jawab:
Soal di atas dapat dikerjakan dengan mengalikan z sebanyak 7 kali.. Tapi, itu sangat buang-buang waktu.. Jadi, kita akan menggunakan dalil de Moivre..
Langkahnya sama seperti nomor 1. Hitung r dan , lalu tinggal masuk ke rumus. ^^
, lalu tinggal masuk ke rumus. ^^



Jadi,



 .
.
Contoh Soal 3:

Tentukan nilai z.
Jawab:
Masih ingatkan notasi ini: .
.
Hal ini juga berlaku untuk , maka persamaan di atas menjadi
, maka persamaan di atas menjadi

Soal di atas dapat ditulis dalam bentuk: .
.

 +
+  (di mana n =0,1,2,3,...)
(di mana n =0,1,2,3,...)
Ingat Dalil De Moivre .. Jika n=3, maka:
.. Jika n=3, maka:
 --->
--->  --->
--->  --->
--->  .
.
 --->
--->  --->
--->  =
=  --->
---> 
Oleh karena itu, kita sekarang sudah mendapatkan z.
z = =
=  =
=  .
.
Dengan mensubstitusikan nilai n=0,1,2, maka kita akan mendapatkan 3 nilai z.
 =
=  =
=  = 2
= 2
 =
=  =
=  =
= 
 =
=  =
=  =
= 
 .
.Hitunglah
 .
.Jawab:
Seandainya kita tidak mau menggunakan dalil de Moivre pun, kita bisa mengerjakan soal ini secara *tradisional*.. Yaitu dengan mengalikannya satu per satu.
 =
=  =
=  =
= 
Nah, bagaimana jika kita ingin mengerjakannnya secara dalil de Moivre? Akan lebih mengerti jika kita menggambar titik z itu.. (Ini supaya kita lebih mengerti saja.. Tapi, tidak mutlak)

 =
= 
 ---->
---->  (karena terletak di kuadran 4...)
(karena terletak di kuadran 4...)
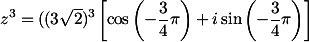
 =
=  .
.Hasilnya sama, bukan?
Contoh Soal 2:

Hitunglah
 .
.Jawab:
Soal di atas dapat dikerjakan dengan mengalikan z sebanyak 7 kali.. Tapi, itu sangat buang-buang waktu.. Jadi, kita akan menggunakan dalil de Moivre..
Langkahnya sama seperti nomor 1. Hitung r dan
 , lalu tinggal masuk ke rumus. ^^
, lalu tinggal masuk ke rumus. ^^


Jadi,



 .
.Contoh Soal 3:

Tentukan nilai z.
Jawab:
Masih ingatkan notasi ini:
 .
.Hal ini juga berlaku untuk
 , maka persamaan di atas menjadi
, maka persamaan di atas menjadi
Soal di atas dapat ditulis dalam bentuk:
 .
.
 +
+  (di mana n =0,1,2,3,...)
(di mana n =0,1,2,3,...)Ingat Dalil De Moivre
 .. Jika n=3, maka:
.. Jika n=3, maka: --->
--->  --->
--->  --->
--->  .
. --->
--->  --->
--->  =
=  --->
---> 
Oleh karena itu, kita sekarang sudah mendapatkan z.
z =
 =
=  =
=  .
.Dengan mensubstitusikan nilai n=0,1,2, maka kita akan mendapatkan 3 nilai z.
 =
=  =
=  = 2
= 2 =
=  =
=  =
= 
 =
=  =
=  =
= 
=========================================================================
Selesai sudah bagian Dalil De Moivre, bilangan kompleks bagian kedua...!! XD
Mudah bukan?? Post ini adalah revisi kedua, setelah sebelumnya ada kesesatan menggunakan dalil De Moivre di mana nilai n-nya boleh pecahan (di contoh soal nomor 3 dan 4).. Ingat, dalil de Moivre hanya berfungsi jika n adalah bilangan bulat.. So, post ini aku rombak ulang agar tidak menggunakan cara yang menyesatkan (meskipun jawaban di post sebelumnya tidak salah, namun ini hanya di dalam kasus khusus yang demikian, dan tidak akan dibahas di sini.) ^^
Bukti: Persamaan euler. ^^
Ini adalah materi lanjutan dari "Bilangan Kompleks...(ii) {Dalil De Moivre}"... Mohon dilihat kembali untuk lebih jelasnya.. ^^.. Dan ini mungkin bisa dikatakan sebagai materi yang rumit bagi kebanyakan mahasiswa di universitasku.. Namun sesungguhnya, kita tidak perlu menjadi profesor untuk membuktikan rumus *dewa* ini, karena bukti itu sekarang sudah jelas di depan mata, dan lagi *bukti ini cukup mudah diturunkan*!!
 Sekali lagi, saya ingatkan.. Jangan kaget bahwa ternyata pembuktian rumus ini sangatlah mudah.. ^^
Sekali lagi, saya ingatkan.. Jangan kaget bahwa ternyata pembuktian rumus ini sangatlah mudah.. ^^
=========================================================================
Ingat konsep awal euler bahwa:

Dengan melihat konsep itu, cobalah untuk menguraikan bentuk .
.
 =
=  =
= 
 =
= 
Kita beri notasi mod. untuk kedua ruas.
 =
=  =
=  =
= 
Kita dapatkan persamaan berikut:
 =
=  <----- diambil dari ruas paling kiri dan kanan. Lalu, kita buat n mendekati tak hingga (agar bisa sesuai dengan konsep awal, konsep euler).
<----- diambil dari ruas paling kiri dan kanan. Lalu, kita buat n mendekati tak hingga (agar bisa sesuai dengan konsep awal, konsep euler). 
 =
= =
= =
= =
= Oleh karena itu:
Oleh karena itu:

 =
=  <----- diambil dari ruas paling kiri dan kanan. Jika ditulis ulang menjadi:
<----- diambil dari ruas paling kiri dan kanan. Jika ditulis ulang menjadi: 
Nah, kita kembali ke persamaan awal, yaitu persamaan di bawah:
 =
= 
Kita beri notasi arg. untuk kedua ruas.
 =
=  =
= 
Kita dapatkan persamaan berikut:
 =
=  <---------- diambil dari ruas paling kiri dan kanan.. Dekati n hingga tak terhingga (agar sesuai dengan konsep awal, konsep euler).
<---------- diambil dari ruas paling kiri dan kanan.. Dekati n hingga tak terhingga (agar sesuai dengan konsep awal, konsep euler).  =
=  =
= =
= 
Oleh karena itu:
 =
=  <----- diambil ruas yang paling kiri dan kanan. Jika ditulis ulang menjadi:
<----- diambil ruas yang paling kiri dan kanan. Jika ditulis ulang menjadi: 
=========================================================================

 Seandainya y positif, maka:
Seandainya y positif, maka:  ... (i)
... (i)
Seandainya y negatif, maka: ... (ii)
... (ii)
Lalu, kita lakukan operasi penjumlahan atau pengurangan pada kedua persamaan:
Dari eliminasi tersebut menghasilkan 2 identitas berikut:
*)
*)
=========================================================================
Ternyata, pembuktian persamaan euler ini cukup mudah.. Hanya memakai konsep limit saja sudah cukup. Tidak perlu mengunakan pengintegralan dan sebagainya...

=========================================================================
PROOF
Bukti ini banyak makan tempat.. Oleh karena itu, saya menggunakan banyak singkatan atau permisalan:




Ingat konsep awal euler bahwa:

Dengan melihat konsep itu, cobalah untuk menguraikan bentuk
 .
. =
=  =
= 
Ingat-ingat kembali.. z jika dinotasikan dalam polar adalah sebagai berikut.
z = [mod.(z)] . cis[arg(z)]
Lalu, ingatlah dalil De Moivre yang bunyinya berikut.

Oleh karena itu, dapat dikatakan bahwa:

Kita tulis ulang dalam bentuk x dan y, maka menjadi:

Lanjuutt. Tadi, kita sudah sampai sini...z = [mod.(z)] . cis[arg(z)]
Lalu, ingatlah dalil De Moivre yang bunyinya berikut.

Oleh karena itu, dapat dikatakan bahwa:

Kita tulis ulang dalam bentuk x dan y, maka menjadi:

 =
= 
Kita beri notasi mod. untuk kedua ruas.
 =
=  =
=  =
= 
Kita dapatkan persamaan berikut:
 =
=  <----- diambil dari ruas paling kiri dan kanan. Lalu, kita buat n mendekati tak hingga (agar bisa sesuai dengan konsep awal, konsep euler).
<----- diambil dari ruas paling kiri dan kanan. Lalu, kita buat n mendekati tak hingga (agar bisa sesuai dengan konsep awal, konsep euler). 
 =
= =
= =
= =
=

 =
=  <----- diambil dari ruas paling kiri dan kanan. Jika ditulis ulang menjadi:
<----- diambil dari ruas paling kiri dan kanan. Jika ditulis ulang menjadi: 
Ingat-ingat kembali.. z jika dinotasikan dalam polar adalah sebagai berikut.
z = [mod.(z)] . cis[arg(z)]
Lalu, ingatlah dalil De Moivre yang bunyinya berikut.

Oleh karena itu, dapat dikatakan bahwa:

Kita tulis ulang dalam bentuk x dan y, maka menjadi:

z = [mod.(z)] . cis[arg(z)]
Lalu, ingatlah dalil De Moivre yang bunyinya berikut.

Oleh karena itu, dapat dikatakan bahwa:

Kita tulis ulang dalam bentuk x dan y, maka menjadi:

Nah, kita kembali ke persamaan awal, yaitu persamaan di bawah:
 =
= 
Kita beri notasi arg. untuk kedua ruas.
 =
=  =
= 
Kita dapatkan persamaan berikut:
 =
=  <---------- diambil dari ruas paling kiri dan kanan.. Dekati n hingga tak terhingga (agar sesuai dengan konsep awal, konsep euler).
<---------- diambil dari ruas paling kiri dan kanan.. Dekati n hingga tak terhingga (agar sesuai dengan konsep awal, konsep euler).  =
=  =
= =
= 
Oleh karena itu:
 =
=  <----- diambil ruas yang paling kiri dan kanan. Jika ditulis ulang menjadi:
<----- diambil ruas yang paling kiri dan kanan. Jika ditulis ulang menjadi: 
Kita sudah mendapatkan  dan
dan  . Selanjutnya, kita kembali ke konsep awal.
. Selanjutnya, kita kembali ke konsep awal.

 Substitusikan
Substitusikan  dan
dan  , maka menjadi:
, maka menjadi:

 dan
dan  . Selanjutnya, kita kembali ke konsep awal.
. Selanjutnya, kita kembali ke konsep awal.

 dan
dan  , maka menjadi:
, maka menjadi:
Terbukti
=========================================================================
KEADAAN KHUSUS
Jika x=0, maka persamaan eulernya menjadi:

 ... (i)
... (i)Seandainya y negatif, maka:
 ... (ii)
... (ii)Lalu, kita lakukan operasi penjumlahan atau pengurangan pada kedua persamaan:
Dari eliminasi tersebut menghasilkan 2 identitas berikut:
*)

*)

=========================================================================
Ternyata, pembuktian persamaan euler ini cukup mudah.. Hanya memakai konsep limit saja sudah cukup. Tidak perlu mengunakan pengintegralan dan sebagainya...
Dasar Teorema Binomial
Apa itu teorema binomial? Lalu, jika kalian sudah tahu, bisakah kalian mengerjakan soal-soal di bawah ini?
Bahasan mengenai teorema binomial di sini tidaklah sulit. Saya sendiri hanya tahu dasarnya saja.
Nah, karena kita saling belajar, makanya kalo ada yang ingin sharing silakan... ^^
Baca lanjutannya di bawah.
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
 dapat ditemukan dari perkalian secara langsung. Dengan mudah, kita bisa mengekspansikan
dapat ditemukan dari perkalian secara langsung. Dengan mudah, kita bisa mengekspansikan  ,
,  , dan selanjutnya seperti di bawah karena pangkatnya cukup kecil.
, dan selanjutnya seperti di bawah karena pangkatnya cukup kecil.
 =
= 
 =
= 
 =
= 
 =
= 
 =
= 
 =
= 
Perhatikan pola dari suku-suku . Pasti selalu dimulai dari suku
. Pasti selalu dimulai dari suku  . (Ini sebetulnya merupakan perjanjian saja). Lalu, suku berikutnya, pangkat dari a akan berkurang 1, namun pangkat dari b akan naik sebesar 1. Jadi, dapat dideskripsikan sebagai berikut.
. (Ini sebetulnya merupakan perjanjian saja). Lalu, suku berikutnya, pangkat dari a akan berkurang 1, namun pangkat dari b akan naik sebesar 1. Jadi, dapat dideskripsikan sebagai berikut.
 =
=  .
. +
+  .
. +
+  .
. + ... +
+ ... +  .
. +
+  .
. .Lalu, untuk menentukan koefisien (c) tiap suku kita dapat menggunakan segitiga Pascal.
.Lalu, untuk menentukan koefisien (c) tiap suku kita dapat menggunakan segitiga Pascal.
_____________________1
__________________1______1_____________==> koefisien untuk
_______________1_____2______1__________==> koefisien untuk
_____________1____3_____3______1________==> koefisien untuk
___________1___4_____6______4____1______==> koefisien untuk _________1___5____10____10_____5____1___==> koefisien untuk
_________1___5____10____10_____5____1___==> koefisien untuk 
______1____6___15____20_____15____6___1_ ==> koefisien untuk
Namun, cara di atas hanya dipakai untuk pangkat yang kecil (sedikit). Sulit untuk menjabarkan segitiga Pascal untuk baris yang sangat banyak (untuk pangkat yang besar). Jadi, kita gunakan kombinasi. Cara untuk mengekspansikan dengan kombinasi inilah yang disebut teorema binomial.
dengan kombinasi inilah yang disebut teorema binomial.
Melalui hubungan kombinasi dengan teorema binomial, maka kita dapat merumuskan ulang rumus teorema binomial sebagai berikut:
 =
= 
atau
 =
=  Kedua rumus di atas identik. Hanya beda penulisan simbol C saja. ^^
Kedua rumus di atas identik. Hanya beda penulisan simbol C saja. ^^
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
Mungkin ini adalah bagian yang ditunggu-tunggu.. Kalau tidak latihan, tidak mungkin jago. Betul? ^^
1. Ekspansikan 
2. Berapakah suku keenam dari ekspansi
3. Berapakah suku yang mengandung dari ekspansi
dari ekspansi 
4. Berapakah koefisien suku dari ekspansi
dari ekspansi 

2. Berapakah suku keenam dari ekspansi

3. Berapakah suku yang mengandung
 dari ekspansi
dari ekspansi 
4. Berapakah koefisien suku
 dari ekspansi
dari ekspansi 
Bahasan mengenai teorema binomial di sini tidaklah sulit. Saya sendiri hanya tahu dasarnya saja.
Nah, karena kita saling belajar, makanya kalo ada yang ingin sharing silakan... ^^
Baca lanjutannya di bawah.
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
Preface
Segitiga Pascal dan Kombinasi
Sebetulnya, Segitiga Pascal dan Kombinasi
 dapat ditemukan dari perkalian secara langsung. Dengan mudah, kita bisa mengekspansikan
dapat ditemukan dari perkalian secara langsung. Dengan mudah, kita bisa mengekspansikan  ,
,  , dan selanjutnya seperti di bawah karena pangkatnya cukup kecil.
, dan selanjutnya seperti di bawah karena pangkatnya cukup kecil. =
= 
 =
= 
 =
= 
 =
= 
 =
= 
 =
= 
Perhatikan pola dari suku-suku
 . Pasti selalu dimulai dari suku
. Pasti selalu dimulai dari suku  . (Ini sebetulnya merupakan perjanjian saja). Lalu, suku berikutnya, pangkat dari a akan berkurang 1, namun pangkat dari b akan naik sebesar 1. Jadi, dapat dideskripsikan sebagai berikut.
. (Ini sebetulnya merupakan perjanjian saja). Lalu, suku berikutnya, pangkat dari a akan berkurang 1, namun pangkat dari b akan naik sebesar 1. Jadi, dapat dideskripsikan sebagai berikut. =
=  .
. +
+  .
. +
+  .
. + ... +
+ ... +  .
. +
+  .
. .
._____________________1
__________________1______1_____________==> koefisien untuk

_______________1_____2______1__________==> koefisien untuk

_____________1____3_____3______1________==> koefisien untuk

___________1___4_____6______4____1______==> koefisien untuk
 _________1___5____10____10_____5____1___==> koefisien untuk
_________1___5____10____10_____5____1___==> koefisien untuk 
______1____6___15____20_____15____6___1_ ==> koefisien untuk

Namun, cara di atas hanya dipakai untuk pangkat yang kecil (sedikit). Sulit untuk menjabarkan segitiga Pascal untuk baris yang sangat banyak (untuk pangkat yang besar). Jadi, kita gunakan kombinasi. Cara untuk mengekspansikan
 dengan kombinasi inilah yang disebut teorema binomial.
dengan kombinasi inilah yang disebut teorema binomial.Hubungan kombinasi dengan teorema binomial
Perhatikan ilustrasi berikut. Dalam aljabar, kita tahu bahwa
 =
=  .Penjabaran dari
.Penjabaran dari  merupakan perkalian dari 3 faktor.
merupakan perkalian dari 3 faktor.
 =
= 

 Lalu, kita pilih bagian yang ingin kita kalikan dari ketiga faktor itu. Misalnya, jika kita memilih a dari setiap faktor dan mengalikannya, maka kita peroleh aaa. Jika kita memilih a dari faktor pertama, a dari faktor kedua dan b dari faktor ketiga kemudian mengalikannya, maka kita peroleh aab, dan seterusnya. Sehingga semua kemungkinan pemilihan baik a maupun b dari masing-masing faktor adalah
Lalu, kita pilih bagian yang ingin kita kalikan dari ketiga faktor itu. Misalnya, jika kita memilih a dari setiap faktor dan mengalikannya, maka kita peroleh aaa. Jika kita memilih a dari faktor pertama, a dari faktor kedua dan b dari faktor ketiga kemudian mengalikannya, maka kita peroleh aab, dan seterusnya. Sehingga semua kemungkinan pemilihan baik a maupun b dari masing-masing faktor adalah
 ;
;  ;
;  ;
;  ;
; ;
;  ;
;  ;
;  Jika semua suku-suku diatas dijumlahkan, maka hasilnya adalah
Jika semua suku-suku diatas dijumlahkan, maka hasilnya adalah
 Bilangan 3 yang merupakan koefisien dari
Bilangan 3 yang merupakan koefisien dari  muncul dari pemilihan a dari 2 faktor dan b dari 1 faktor sisanya. Hal ini bisa dilakukan dalam
muncul dari pemilihan a dari 2 faktor dan b dari 1 faktor sisanya. Hal ini bisa dilakukan dalam  atau
atau  cara. Cara yang sama bisa dilakukan untuk memperoleh koefisien
cara. Cara yang sama bisa dilakukan untuk memperoleh koefisien  yang dalam hal ini merupakan pemilihan a dari 0 faktor dan b dari 3 faktor lainnya yang dapat dilakukan dalam
yang dalam hal ini merupakan pemilihan a dari 0 faktor dan b dari 3 faktor lainnya yang dapat dilakukan dalam  atau
atau  cara, dan seterusnya.
cara, dan seterusnya.
Perhatikan ilustrasi berikut. Dalam aljabar, kita tahu bahwa
 =
=  .
. merupakan perkalian dari 3 faktor.
merupakan perkalian dari 3 faktor. =
= 


aaa; aab; aba; abb; baa; bab; bba; bbb
Jika dikalikan menjadi: ;
;  ;
;  ;
;  ;
; ;
;  ;
;  ;
; 

 muncul dari pemilihan a dari 2 faktor dan b dari 1 faktor sisanya. Hal ini bisa dilakukan dalam
muncul dari pemilihan a dari 2 faktor dan b dari 1 faktor sisanya. Hal ini bisa dilakukan dalam  atau
atau  cara. Cara yang sama bisa dilakukan untuk memperoleh koefisien
cara. Cara yang sama bisa dilakukan untuk memperoleh koefisien  yang dalam hal ini merupakan pemilihan a dari 0 faktor dan b dari 3 faktor lainnya yang dapat dilakukan dalam
yang dalam hal ini merupakan pemilihan a dari 0 faktor dan b dari 3 faktor lainnya yang dapat dilakukan dalam  atau
atau  cara, dan seterusnya.
cara, dan seterusnya.Melalui hubungan kombinasi dengan teorema binomial, maka kita dapat merumuskan ulang rumus teorema binomial sebagai berikut:
 =
= 
atau
 =
= 
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
Bagian II
Latihan
Latihan
Mungkin ini adalah bagian yang ditunggu-tunggu.. Kalau tidak latihan, tidak mungkin jago. Betul? ^^
| 1. | Ekspansikan  Jawab: Jika memakai cara rumit, bisa saja kita menghitung dengan cara mengalikan  sebanyak 6 kali. Tapi, karena rumit, kita gunakan teorema binomial. sebanyak 6 kali. Tapi, karena rumit, kita gunakan teorema binomial. = =  . . + +  . .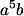 + +  . . + +  . . + +  . . + +  . . + +  . . Ingat bahwa:   = =  . . + +  . .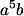 + +  . . + +  . . + +  . . + + 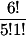 . . + +  . . ______=  + 6 + 6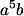 + 15. + 15. + 20. + 20. + 15. + 15. + 6. + 6. + +  Perhatikan sifat-sfat yang timbul dari penjabaran tersebut: 1. Banyaknya suku adalah (n+1) = 6+1 = 7. 2. Jumlah dari eksponen a dan b dalam setiap suku adalah n. |
| 2. | Ekspansikan  Jawab: Tidak berbeda jauh dengan soal sebelumnya. Jika memakai simbol  , anggap a = , anggap a =  , b = , b =  , dan n=5. , dan n=5. = =  . . + +  . . . . + +  . . . . + +  . . . . + +  . . . . + +   ______ =  + 5.2. + 5.2.  + 10.4. + 10.4. 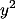 + 10.8. + 10.8.  + 5.16. + 5.16.  + 32 + 32 ______ =  + 10 + 10  + 40 + 40 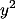 + 80 + 80  + 80 + 80  + 32 + 32 |
| 3. | Ekspansikan  Jawab: Soal di atas, tak jauh berbeda dengan soal nomor 2... <==males bikin soal. Jika memakai simbol  , anggap a = , anggap a =  , b = , b =  , dan n=5. , dan n=5. = =  + +   + +   + +   + +   + +  ______ =   5.2. 5.2.  + 10.4. + 10.4. 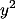  10.8. 10.8.  + 5.16. + 5.16.   32 32 ______ =   10 10  + 40 + 40 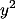  80 80  + 80 + 80   32 32 Perhatikan jawaban di atas. Ternyata menghasilkan suku-suku ganjil dan genap secara berseling. |
| 4. | Berapakah suku keenam dari ekspansi  Jawab: Suku keenamnya =    Suku keenamnya =    Suku keenamnya = 3.7.6.     Suku keenamnya =  |
| 5. | Berapakah suku ke-4 dari ekspansi  Jawab: Suku ke-4=    Suku ke-4=      Suku ke-4=  Suku ke-4=  |
| 6. | Berapakah suku ke-7 dari ekspansi  Jawab: Karena pangkatnya 5, maka jumlah sukunya hanya ada = 5+1 = 6. Jadi,  tidak memiliki suku ke-7. tidak memiliki suku ke-7. |
| 7. | Berapakah suku yang mengandung  dari ekspansi dari ekspansi  Jawab: Ini hanya soal jebakan. Pangkat terkecil hasil penjabaran adalah  . .Jadi, ekspansi  tidak memiliki suku yang mengandung tidak memiliki suku yang mengandung  . . |
| 8. | Berapakah koefisien suku yang mengandung  dari ekspansi dari ekspansi  Jawab: Kombinasi yang mungkin untuk  adalah: adalah: = =  dimana p+q = 10 dimana p+q = 10Note: Di atas, koefisien tidak berpengaruh dalam pembentukan  . Jadi dapat dihilangkan.. . Jadi dapat dihilangkan..(i)... p + 3q = 14 dimana p+q = 10 ...(ii) Dari 2 persamaan tersebut, gunakan eliminasi/substitusi biasa, sehingga didapatq = 2 dan p = 8 Karena q=2, maka dari sini kita tahu bahwa suku yang dicari adalah suku ke(2+1)=3. Kita memilih q (bukan p) karena q merupakan eksponen b dari  yang langsung menunjuk ke suku mana penjabaran itu didapat. yang langsung menunjuk ke suku mana penjabaran itu didapat.Suku ke-3=    Suku ke-3=  .4. .4.  Suku ke-3= 180  Berarti koefisien suku yang mengandung  dari ekspansi dari ekspansi  = 180. = 180. |
| 9. | Berapakah koefisien suku yang mengandung  dalam ekspansi dalam ekspansi  Jawab: (Soal ini hanya untuk memperjelas soal di sebelumnya saja)  terbentuk dari kombinasi antara terbentuk dari kombinasi antara  dan dan  . . = =  dimana p+q =14 dimana p+q =14 = =  dimana p+q =14 dimana p+q =14(i)...  p + 2q = 4 dimana p+q =14 ...(ii) p + 2q = 4 dimana p+q =14 ...(ii)Setelah kedua persamaan disubstutusi/ di eliminasi, maka didapat p = 8 dan q=6 q menunjuk  (elemen kedua dalam (elemen kedua dalam  ). ).q = 6. Berarti, kita harus mencari suku ke-(6+1) = 7 Suku ke-7 =    Suku ke-7 =      Suku ke-7 =   |
| 10. | Tentukan koefisien dari  dalam ekspansi dalam ekspansi  Jawab: Asumsikan kejadian ini sebagai 3 aktivitas. Pertama memilih a dari 2 faktor diantara 11 faktor yang bisa dilakukan dalam  cara. Kedua, memilih b dari 3 faktor diantara 9 faktor yang bisa dilakukan dalam cara. Kedua, memilih b dari 3 faktor diantara 9 faktor yang bisa dilakukan dalam  cara. Ketiga, memilih c dari 6 faktor diantara 6 faktor sisanya yang bisa dilakukan dalam cara. Ketiga, memilih c dari 6 faktor diantara 6 faktor sisanya yang bisa dilakukan dalam  cara. Jadi, jika semuanya dikalikan, maka koefisien untuk cara. Jadi, jika semuanya dikalikan, maka koefisien untuk  didapat. didapat.Koefisien untuk  = =    = 4620 = 4620 |
| 11. | Berapakah koefisien suku  dari ekspansi dari ekspansi  Jawab: Seperti soal sebelumnya, namun di sini hanya ada 1 variabel, yaitu x. Artinya, akan ada banyak kemungkinan yang timbul. Logika memecahkan soal ini mirip seperti soal nomor 8 atau 9. Pertama, kita temukan terlebih dahulu kombinasi yang mungkin untuk membentuk  . .Kombinasi yang mungkin untuk membentuk  : : = k. = k.  dimana dimana   Maka, kedua persamaan sekarang menjadi: (i)... 5q + 9r = 23 dimana Karena nilai q dan harus bulat positif, kita dapat dengan mudah menyelesaikan persamaan 5q + 9r = 23 dengan menggunakan cara persamaan linear diophantine atau cara coba-coba. Setelah dikerjakan dengan cara coba-coba, maka didapat hasilnya ... (ii) ... (ii)q = 1 dan r = 2. Maka, p = 100-2-1 = 97. 5 x 1 + 9 x 2 = 23 Maka, suku yg mengandung  = =       _______________________=  _______________________= 49  Jadi, koefisiennya adalah 49. |
| 12. | Tentukan koefisien suku yang mengandung  dalam ekspansi dalam ekspansi  Jawab: Cara mengerjakan soal ini sama seperti sebelumnya. Pertama, tentukan terlebih dahulu kombinasi yang mungkin untuk  . . = =  di mana p+q+r = 15 di mana p+q+r = 15-p + q + 2r = 5 di mana p+q+r = 15 Ada 2 persamaan yang diperoleh:2r + q - p = 5 ... (i) p+q+r = 15 ... (ii) Kita harus berusaha mendapatkan pasangan p,q,dan r yang memenuhi kedua kendala itu. Bisa dengan menggunakan persamaan linear diophantine atau coba-coba. Di sini, kita gunakan cara coba-coba. Pertama, ubah persamaan (ii) menjadi p = 15-q-r lalu substitusikan ke persamaan (i) 2r + q - (15-q-r) = 5 3r + 2q = 20 Karena nilai r dan q harus positif, maka  . Lalu, perhatikan bahwa 2q dan 20 adalah bilangan genap, maka 3r juga haruslah genap. Jadi, kita sekarang mendapatkan 4 kemungkinan r, yaitu 0, 2, 4, dan 6. . Lalu, perhatikan bahwa 2q dan 20 adalah bilangan genap, maka 3r juga haruslah genap. Jadi, kita sekarang mendapatkan 4 kemungkinan r, yaitu 0, 2, 4, dan 6.Jika r = 0 ==> q = 10 ==> p=5 Jika r = 2 ==> q = 7 ==> p=6Jika r = 4 ==> q = 4 ==> p=7Jika r = 6 ==> q = 1 ==> p=8 Jadi, jumlah suku yang mengandung  = =       + +       + +     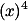  + +   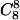    = (3003 + 180180 + 450450 + 5014 ) = (3003 + 180180 + 450450 + 5014 )  = 638647 = 638647  Jadi, koefisiennya adalah 638647.. (Maap angkanya jelek) |
| 13. | Tentukan nilai dari  Jawab: Ingat teorema binomial bahwa:  = =  Jika kita mensubstitusikan a =1 dan b =1, maka hasilnya menjadi berikut:  = =   = =  Jika kita mensubstitusikan n=2009, maka jawaban dari soal akan diperoleh.  = =  |
| 14. | Jika A = banyaknya suku dari ekspansi  B = banyaknya suku dari ekspansi  Maka, berapakah selisih A dan B? Jawab: Banyaknya suku dari ekspansi  adalah adalah  . .Di rumus di atas, n adalah pangkat, sedangkan v adalah jumlah variabel. == Di sini, tidak akan dijelaskan penurunan rumusnya. Alasannya, karena saya sendiri baru dapet rumus itu secara tidak sengaja pas ngerjain soal beginian.. Tapi, aku yakin, rumus ini sudah ditemukan dari dulu-dulu.. Ada yang bisa menurunkannya? ==  memiliki v = 4 dan n=6, maka memiliki v = 4 dan n=6, makaA =  = 84. = 84. memiliki v=5 dan n=4, maka memiliki v=5 dan n=4, makaB =  = 70. = 70.Maka, A - B = 84 - 70 = 14. Artinya,  memiliki suku lebih banyak daripada memiliki suku lebih banyak daripada  . . |
http://wapedia.mobi/id/Special:Search?search=bilangan+kompleks&skl=Tuju+ke&searchtype=
http://hendrydext.blogspot.com/2008/12/bilangan-kompleks-ii-dalil-de-moivre.html















Tidak ada komentar:
Posting Komentar
Catatan: Hanya anggota dari blog ini yang dapat mengirim komentar.