A. Pentingnya Kontrol
- Untuk memastikan bahwa CBIS telah diimplementasikan seperti yang direncanakan, system beroperasi seperti yang dikehendaki, dan operasi tetap dalam keadaan aman dari penyalahgunaan atau gangguan.
- Untuk memberi dukungan kepada manajer dalam mengontrol area operasinya
B. Tugas Kontrol CBIS
Mencakup semua fase siklus hidup, selama siklus hidup dibagi menjadi kontrol-kontrol yang berhubungan dengan pengembangan sistem, desain dan operasi
- Metode Untuk Mendapatkan dan Memelihara Kontrol CBIS
2. Manajemen mengontrol CBIS secara tidak langsung dengan terus menerus melalui CIO.
3. Manajemen mengontrol CBIS secara tidak langsung berkenaan dengan proyeknya melalui pihak ketiga
AREA PENGONTROLAN CBIS
- Kontrol Proses Pengembangan
* Fase Perencanaan
Mendefinisikan tujuan dan kendala
* Fase Analisis & Disain
> Mengidentifikasi kebutuhan informasi
> Menentukan kriteria penampilan
> Menyusun disain dan standar operasi CBIS
* Fase Implementasi
> Mendefinisikan program pengujian yang dapat diterima
> Memastikan apakah memenuhi criteria penampilan
> Menetapkan prosedur utk memelihara CBIS
* Fase Operasi & Kontrol
> Mengontrol CBIS selagi berevolusi selama fase SLC
> Memastikan bahwa CBIS yang diimplementasikan dapat memenuhi kebutuhan
Yang termasuk dalam kontrol proses pengembangan, yaitu :
1. Manajemen puncak menetapkan kontrol proyek secara keseluruhan selama fase perencanaan dengan cara membentuk komite MIS
2. Manajemen memberitahu pemakai mengenai orientasi CBIS
3. Manajemen menentukan kriteria penampilan yang digunakan dalam mengevaluasi operasi CBIS.
4. Manajemen dan bagian pelayanan informasi menyusun disain dan standar CBIS
5. Manajemen dan pelayanan informasi secara bersama-sama mendefinisikan program pengujian yang dapat diterima
6. Manajemen melakukan peninjauan sebelum instalasi yang dilakukan tepat setelah penggantian dan secara berkala meninjau CBIS untuk memastikan apakah ia memenuhi kriteria penampilan.
7. Bagian pelayanan informasi menetapkan prosedur untuk memelihara dan memodifikasi CBIS dan prosedur yang disetujui oleh manajemen.
- Kontrol Disain Sistem
* Kontrol tidak boleh diterapkan jika biayanya lebih besar dari manfaatnya. Nilai atau manfaat adalah tingkat pengurangan resiko.
* Selama fase disain dan analisis dari siklus hidup system, Analis System, DBA dan Manajer Jaringan membangun fasilitas kontrol tertentu dalam disain system. Selama fase implementasi, programmer menggabungkan kontrol tersebut ke dalam system. Disain system dikontrol dengan cara menggabungkan kontrol software menjadi lima bagian pokok, yaitu :
I. Permulaan Transaksi (Transaction Origination)
* Tahap-tahap yang harus dilakukan pada permulaan transaksi :1. Permulaan Dokumentasi Sumber
> Perancangan dokumentasi
> Pemerolehan dokumentasi
> Kepastian keamanan dokumen
2. Kewenangan
> Bagaimana entry data akan dibuat menjadi dokumen dan oleh siapa
3. Pembuatan Input Komputer
> Mengidentifikasi record input yang salah dan memastikan semua data input
diproses
4. Penanganan Kesalahan
> Mengoreksi kesalahan yang telah dideteksi dan menggabungkan record yg telah dikoreksi ke record entry
5. Penyimpanan Dokumen Sumber
> Menentukan bagaimana dokumen akan disimpan dan dalam kondisi
bagaimana dapat dikeluarkan
II. Entri Transaksi
* Entri transaksi mengubah data dokumen sumber menjadi bentuk yang dapat dibaca oleh komputer. Kontrol ini berusaha untuk menjaga keakuratan data yang akan ditransmisikan ke jaringan komunikasi atau yang akan dimasukkan secara langsung ke dalam komputer. Area kontrolnya meliputi atas :1. Entri Data
> Kontrol dalam bentuk prosedur tertulis dan dalam bentuk peralatan inputnya sendiri. Dapat dilakukan dengan proses offline/online
2. Verifikasi Data
> Key Verification (Verifikasi Pemasukan)
Data dimasukkan ke sistem sebanyak 2 kali
> Sight Verification (Verifikasi Penglihatan)
Melihat pada layar sebelum memasukkan data ke system
3. Penanganan Kesalahan
> Merotasi record yang telah dideteksi ke permulaan transaksi untuk pengoreksian
4. Penyeimbangan Batch
> Mengakumulasikan total setiap batch untuk dibandingkan dengan total yang sama yang dibuat selama permulaan transaksi
III. Komunikasi Data
* Tanggungjawab manajer jaringan dengan menggabungkan ukuran keamanan ke dalam sistem dan memonitor penampilan untuk memastikan keamanan telah dilakukan dgn baik* Komputer yang ada dalam jaringan memberikan peluang risiko keamanan yang lebih besar dari pada komputer yang ada di dalam suatu ruangan. Area kontrol ini terdiri dari :
1. Kontrol Pengiriman Data
2. Kontrol Channel Komunikasi
3. Kontrol Penerimaan Pesan
4. Rencana Pengamanan Datacom Secara Keseluruhan
IV. Pemrosesan Komputer
* Pada umumnya semua elemen kontrol pada disain system selalu dikaitkan dengan pemasukan data ke dalam komputer. Area kontrol pada pemrosesan komputer terdiri dari :1. Penanganan Data
2. Penanganan Kesalahan
3. Database dan Perpustakaan Software
* Sebagian besar kontrol database dapat diperoleh melalui penggunaan Sistem Manajemen Database (Database Management System/DBMS)
* Tingkat keamanan dalam DBMS terdiri dari :
1. Kata kunci (Password)
2. Direktori pemakai (User Directory)
3. Direktori elemen data (Field Directory)
4. Enkripsi (Encryption)
V. Output Komputer
* Komponen subsistem ini bertanggung jawab untuk mengirimkan produk (output) kepada pemakai (user). Yang termasuk dalam area ini adalah :1. Distribusi
> Kontrol pada distribusi laporan berusaha untuk memastikan ketepatan orang yang menerima output.
2. Penyeimbangan Departemen Pemakai
> Bila departemen pemakai menerima output dari komputer, maka keseluruhan kontrol dari output dibandingkan dengan total yang sama yang telah ditetapkan pada waktu pertama kali data input dibuat.
3. Penanganan Kesalahan
Kelompok kontrol tertentu dapat ditetapkan didalam area pemakai dengan menjalankan prosedur formal untuk mengoreksi kesalahan.
4. Penyimpangan Record
> Tujuan komponen kontrol yang terakhir ini adalah untuk memelihara keamanan yang tepat terhadap output komputer dan untuk mengontrol penyelesaian yang sia-sia.
5. Penyeimbangan Operasi Komputer
> Kontrol ini memungkinkan pelayanan informasi untuk memverifikasi bahwa semua batch dan transaksi yang diterima dari departemen pemakai telah diproses.
- Kontrol Terhadap Pengoperasian Sistem
Kontrol yang memberikan kontribusi terhadap tujuan ini dapat diklasifikasikan menjadi 5 area :
1. Struktur organisasional
> Staf pelayanan informasi diorganisir menurut bidang spesialisasi. Analisis, Programmer, dan Personel operasi biasanya dipisahkan dan hanya mengembangkan ketrampilan yang diperlukan untuk area pekerjaannya sendiri.
2. Kontrol perpustakaan
> Perpustakaan komputer adalah sama dengan perpustakaan buku, dimana didalamnya ada pustakawan, pengumpulan media, area tempat penyimpanan media dan prosedur untuk menggunakan media tersebut. Yang boleh mengakses perpustakaan media hanyalah pustakawannya.
3. Pemeliharaan Peralatan
> Orang yang tugasnya memperbaiki computer yang disebut Customer Engineer (CE) / Field Engineer (FE) / Teknisi Lapangan menjalankan pemeliharaan yang terjadwal / yang tak terjadwal.
4. Kontrol lingkungan dan keamanan fasilitas
> Untuk menjaga investasi dibutuhkan kondisi lingkungan yang khusus seperti ruang computer harus bersih keamanan fasilitas yang harus dilakukan dengan penguncian ruang peralatan dan komputer.
5. Perencanaan disaster
* Rencana Keadaan darurat
> Prioritas utamanya adalah keselamatan tenaga kerja perusahaan
* Rencana Backup
> Menjelaskan bagaimana perusahaan dapat melanjutkan operasinya dari ketika terjadi bencana sampai ia kembali beroperasi secara normal.
* Rencana Record Penting
> Rencana ini mengidentifikasi file data penting & menentukan tempat penyimpanan kopi duplikat.
* Rencana Recovery
> Rencana ini mengidentifikasi sumber-sumber peralatan pengganti, fasilitas komunikasi dan pasokan-pasokan


 ,
,  ,
,  , dan masih banyak lagi..
, dan masih banyak lagi.. . Kita definisikan bahwa
. Kita definisikan bahwa  , maka:
, maka: , maka dapat ditulis sebagai
, maka dapat ditulis sebagai 
 =
=  =
=  = (
= (
 =
= =
=  =
= 
 , tentukan x dan y. Lalu, gambarkan z dalam bidang kompleks!
, tentukan x dan y. Lalu, gambarkan z dalam bidang kompleks!



 .
.
 ,
,  , dan masih banyak lagi.. Tapi, ini yang masih menjadi kendala.. Apakah
, dan masih banyak lagi.. Tapi, ini yang masih menjadi kendala.. Apakah  = ....
= ....




 .
. dapat digambarkan dalam bidang kompleks. Artinya, kita dapat menggambarkannya secara kartesius maupun polar!! Lihat gambar di bawah untuk lebih jelasnya!
dapat digambarkan dalam bidang kompleks. Artinya, kita dapat menggambarkannya secara kartesius maupun polar!! Lihat gambar di bawah untuk lebih jelasnya!

 )
)






















 .
. , maka kita akan menemukan dalil de Moivre:
, maka kita akan menemukan dalil de Moivre:
 .. Cobalah sendiri.. ^^
.. Cobalah sendiri.. ^^ atau
atau  .
. .
. .
. =
=  =
= 

 =
= 
 ---->
---->  (karena terletak di kuadran 4...)
(karena terletak di kuadran 4...)
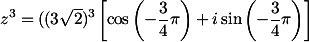

 .
.






 .
.
 , maka persamaan di atas menjadi
, maka persamaan di atas menjadi
 .
.
 +
+  (di mana n =0,1,2,3,...)
(di mana n =0,1,2,3,...) --->
--->  --->
--->  --->
--->  .
. --->
--->  --->
---> 
 =
=  .
. =
=  =
=  =
=  =
=  =
=  =
= 
 =
=  =
=  =
= 




 .
. =
= 



 =
=  =
=  =
= 

 =
= =
= =
=



 =
=  =
= 
 =
=  =
= =
= 

 dan
dan  . Selanjutnya, kita kembali ke konsep awal.
. Selanjutnya, kita kembali ke konsep awal.




 ... (ii)
... (ii)




 dari ekspansi
dari ekspansi 
 dari ekspansi
dari ekspansi 
 dapat ditemukan dari perkalian secara langsung. Dengan mudah, kita bisa mengekspansikan
dapat ditemukan dari perkalian secara langsung. Dengan mudah, kita bisa mengekspansikan  ,
,  , dan selanjutnya seperti di bawah karena pangkatnya cukup kecil.
, dan selanjutnya seperti di bawah karena pangkatnya cukup kecil. =
= 


 =
= 
 =
=  =
= 
 . (Ini sebetulnya merupakan perjanjian saja). Lalu, suku berikutnya, pangkat dari a akan berkurang 1, namun pangkat dari b akan naik sebesar 1. Jadi, dapat dideskripsikan sebagai berikut.
. (Ini sebetulnya merupakan perjanjian saja). Lalu, suku berikutnya, pangkat dari a akan berkurang 1, namun pangkat dari b akan naik sebesar 1. Jadi, dapat dideskripsikan sebagai berikut. .
. .
. +
+  .
. + ... +
+ ... +  .
. +
+  .
. .
.

 ;
;  ;
;  ;
;
 atau
atau  cara. Cara yang sama bisa dilakukan untuk memperoleh koefisien
cara. Cara yang sama bisa dilakukan untuk memperoleh koefisien  atau
atau  cara, dan seterusnya.
cara, dan seterusnya.


 .
. +
+  .
.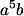 +
+  .
. +
+  .
. +
+  .
. +
+  .
. +
+  .
.

 .
. .
. .
. .
. .
.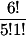 .
. .
. ,
,  , dan n=
, dan n= .
. +
+  .
. .
. .
. .
. +
+  .
. .
. +
+  .
. +
+ 


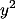




 , dan n=
, dan n= +
+ +
+ +
+






















 .
. dari ekspansi
dari ekspansi 
 =
= 


 .
. dalam ekspansi
dalam ekspansi 
 dan
dan  .
. =
=  =
= 








 dalam ekspansi
dalam ekspansi 
 cara. Kedua, memilih b dari 3 faktor diantara 9 faktor yang bisa dilakukan dalam
cara. Kedua, memilih b dari 3 faktor diantara 9 faktor yang bisa dilakukan dalam  cara. Ketiga, memilih c dari 6 faktor diantara 6 faktor sisanya yang bisa dilakukan dalam
cara. Ketiga, memilih c dari 6 faktor diantara 6 faktor sisanya yang bisa dilakukan dalam  cara. Jadi, jika semuanya dikalikan, maka koefisien untuk
cara. Jadi, jika semuanya dikalikan, maka koefisien untuk  =
= 









 dalam ekspansi
dalam ekspansi 
 =
=  . Lalu, perhatikan bahwa
. Lalu, perhatikan bahwa 




 +
+ 




 +
+ 



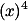
 +
+ 

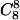


 = (
= (

 =
= 
 =
= 



 adalah
adalah  .
. =
=  =
=